所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。本文就把GMAT数学排列组合知识点介绍。
一、排列组合定义：If you select member after member from the same group, the number of possible choices will decrease by 1 for each choice. Some counting problems involve permutations. A permutation of a set is a reordering of the elements in the set.
排列的定义及其计算公式：从n个不同元素中，任取m(m≤n,m与n均为自然数,下同)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号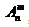
表示。
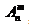=n(n-1)(n-2)……(n-m+1)= n!/(n-m)!
If the order in which the members are chosen makes no difference, the counting problem involves combinations.
组合的定义及其计算公式：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号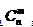
表示。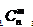
=
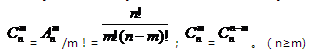
二、加法原理和乘法原理
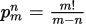
从m个人中挑出n个人进行排列的可能数。
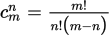
从m个人中挑出n个人进行组合的可能数。
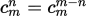
(1)加法原理
某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由n中方法完成，则这件事可由m+n种方法来完成。
例：到美利坚去，既可以乘飞机，也可以坐轮船，其中飞机还有战斗机与民航，轮船有小鹰号和泰坦尼克号，问有多少种走法?
(2)乘法原理
某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n中方法完成，则这件事可由m x n种方法来完成。
例：到美利坚去，先乘飞机，再坐轮船，其中飞机还有战斗机与民航，轮船有小鹰号和泰坦尼克号，问有多少种走法?
三、排列组合真题解析
例题1：
A = {2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
Two integers will be randomly selected from the sets above, one integer from set A and one integer from set B.What is the probability that the sum of the two integers will equal 9 ?
A0.15
B0.20
C0.25
D0.30
E0.33
解析：要使和为9，有(2、7)，(3、6)，(4、5)，(5、4)4种情况
而分别从集合A、B里随机挑选1个数字的概率为4*5，
所以概率为4/(4*5)=0.2
例题2： There are 8 teams in a certain league and each team plays each of the other teams exactly once. If each game is played by 2 teams, what is the total number of games played?
A15
B16
C28
D56
E64
解析：一个社团里有8个队，每个队只和其他队玩一次游戏。问如果2个队玩一种游戏，那么可以玩多少种游戏
C(2，8)=8*7/2=28
》》点击了解GMAT数学复习技巧之排列组合题
以上便是百利天下小编为大家介绍的GMAT数学排列组合知识点介绍，希望大家在以后的GMAT考试备考中能够掌握这些知识，相信通过大家细心努力备考在接下来的GMAT考试中一定会取得满意的GMAT数学成绩。
您还可能关注：
