GMAT数学中的几何陷阱题,题目本身的难度并不高,甚至可以说十分简单,而对于考生来说唯一的难度,就是避免轻视和想当然的态度,准确发现陷阱并加以避免,所以在这里小编就给大家介绍下GMAT数学常见几何考题解析。
一、几何定理须知
1. 直角三角形勾股定理
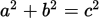
2. 两直线平行,内错角相等,同位角相等。
3. 圆心角是圆周角的两倍。
4. 面积与周长。
① 三角形(边长为a,b,c),面积=1/2 absinγ(γ是a,b两边之夹角)
对于直角三角形,γ=90°,
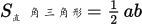
对于等边三角形,γ=60°,

周长=a+b+c
② 梯形(上底为a,下底为b,高为h)
面积=
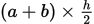
③ 平行四边形(边长为a,b,高为h)
面积=a×h
周长=2(a+b)
④ 矩形(边长为a,b)
面积=a×b
周长=2(a+b)
⑤ 正方形(边长为a)
面积=a2
周长=4a
⑥ 圆(半径为R)
面积=πR2
周长=2πR
5. 多边形内角和
(n-2)180º
二、几何做题须知
几何题之所以容易做错,主要原因便在于题目中给出的参考图片。很多同学可能并不清楚的一点是,这些几何图形,很多都并不是按照题目实际要求画出的,图形大小比例,都可能存在一定的误区,是出题者故意为之。比如给出一个看似等边的三角形图形,实际却可能是各种不规则的三角形。考生如果轻信了题目的几何图,很有可能就会因此产生错误的印象,或脑补出并不存在的条件,或因此看错一些数据,最终计算出错误的答案。
三、几何真题解析
In △PQR, if PQ = x, QR = x+2, and PR= y, which of the three angles of △PQR has the greatest degree
measure?
(1) y = x+3
(2) x = 2
A Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C BOTH statement TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D EACH statement ALONE is sufficient.
E Statements (1) and (2) TOGETHER are NOT sufficient.
解析:要判断△PQR哪个角最大,即需要判断三角形哪条边最长,因为大边对大角。
条件一 y=x+3,那么PQ=x QR=x+2 PR=x+3 所以PR所对应的角最大 即∠PQR最大,充分
条件二 x=2 可以求出PQ=2 QR=5 但是PR与另外边什么关系 无法求出,所以无法求出哪个角最大,不充分,所以选A
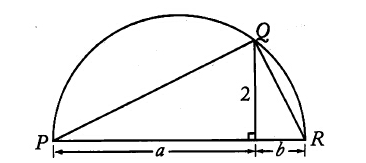
If arc PQR above is a semicircle, what is the length of diameter PR ?
(1) a = 4
(2) b = l
A Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C BOTH statement TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D EACH statement ALONE is sufficient.
E Statements (1) and (2) TOGETHER are NOT sufficient.
解析:求PR的长度
条件一 a=4 设PR中间的那个点为O,那么 由图可知 △PQO∽△QOR 所以a/2=2/b 所以b=1 所以PR=5 充分
条件二 b=1 同理可知 a/2=2/b a=4 PR也可以求出来 充分 所以选D
》》点击了解GMAT数学突破51分必备题目分析之几何
以上就是关于GMAT数学常见几何考题解析的相关介绍,希望大家能够学习。考生千万要注意,争取不要大意失分,更多关于GMAT语法知识点的介绍小编会为大家呈现。最后祝大家顺利备考GMAT考试,早日梦圆名校。
您还可能关注:



