解析几何说到底就一个计算,它本身就是为了解决平面几何问题而建立的体系,考得就是谁算得准,算得快,所以你要尽量减少计算的步骤和时间,才能更快更准,这就需要平面几何的知识,有时候用上了,题目会变的非常简单。今天我们就把GMAT数学的解析几何知识点介绍下。
1. 关于对称。
① 坐标(a,b)关于y=x的对称点为(b,a)
② 坐标(a,b)关于y=-x的对称点为(-b,-a)
2. 直线方程。
① y=kx+b (斜截式，k为斜率slope，b为截距intercept)
②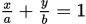 
(截距式，a为x轴上截距，b为y轴上截距)
③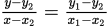 
(两点式，已知
)
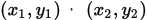④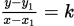 
(点斜式，已知(
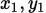)，斜率k)
3、【平面直角坐标系(Plane rectangular coordinate system)】
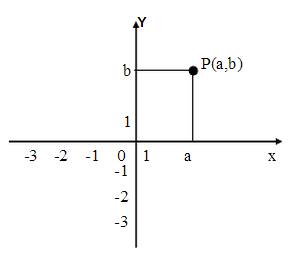
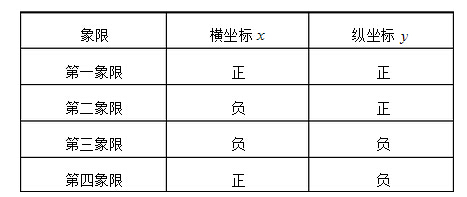
1)点的几何意义点(a,b)到x轴的距离为 |y|;点(a,b)到y轴的距离为 |x|;点(a,b)到坐标原点的距离为
2)点的对称特征：已知点P(a,b), 关于x轴的对称点坐标是(a,-b), 横坐标相同，纵坐标反号 关于y轴的对称点坐标是(-a,b), 纵坐标相同，横坐标反号 关于原点的对称点坐标是(-a,-b) 横，纵坐标都反号
例题：OG15-P180-202
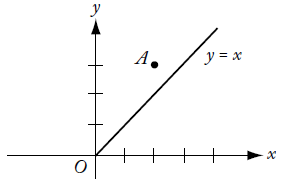
In the rectangular coordinate system above, the line y = x is the perpendicular bisector of segment AB (not shown), and the x-axis is the perpendicular bisector of segment BC (not shown). If the coordinates of point A are (2,3), what are the coordinates of point C ?A (-3,-2)B (-3,2)C (2,-3)D (3,-2)E (2,3)解析：如图所示，y=x垂直平分AB，x轴垂直平分BC，如果A的坐标为(2,3)，那么C的坐标为?这道题最简便的方法为作图，然后观察，象限即其长度大小 即可得到C的坐标为(3,-2)另外也可以根据垂直平分的性质作答。AB的斜率为-1 所以 所在直线为y=-x+5 与y=x相交的点为(2.5，2.5)再根据中点坐标(2+x)/2=2.5 (3+y)/2=2.5 可知 B点坐标为(3,2)所以关于x轴对称的C点坐标即为(3，-2)例题：OG16-P182-210
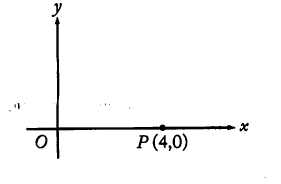
In the rectangular coordinate system above, if point R (not shown) lies on the positive y axis and the area of triangle ORP is 12, what is the y-coordinate of point R?A 3B 6C 9D 12E 24解析：已知直角坐标系中，R在y轴的正半轴上，△ORP的面积为12，求R的纵坐标因为△ORP的面积=1/2*4*y=12 所以 y=6 选B
》》点击了解GMAT数学常见几何考题解析
以上就是关于GMAT数学的解析几何知识点的内容介绍，希望考生通过以上内容，不断夯实自己的知识点，熟练做题技巧，提升解题能力以及分析能力，争取都能取得理想成绩。
您还可能关注：
