几何是GMAT数学的考试一部分内容,但是考点设计的题型都很简单,不过还会有一些考生因为几何图形没看明白与正确失之交臂,那就是很多专业术语搞不明白,本次课程就给大家介绍下GMAT数学突破51分必备题目分析之几何。
一、plane geometry(平面几何)
1、right angle直角
2、Acute angle锐角
3、Obtuse angle钝角
4、Equilateral triangle等边三角形
5、Isosceles triangle 等腰三角
6、Right triangle直角三角形
7、Perimeter 周长
8、Area 面积
例1:
The perimeter of a certain isosceles right triangle is 16+16√2,what is the length of the hypotenuse of the triangle?
题干意思:一个等腰直角三角形的周长是16+16√2,那么斜边长是多少?
分析:等腰直角三角形假设边长分别是a,a,b,那么2a+b=16+16√2,另外b=a√2,所以斜边算出是16.
例2:
If two sides of a triangle have lengths 2 and 5,which of the following could be the perimeter of the triangle?
题干意思:一个三角形的两边分别是2和5,那么周长可能是哪个?
选项一9.选项二15,选项三19.
分析:三角形两边之和大于第三边,两边之差小于第三边,假设第三边是x,那么x 应该是
3
9、circle 圆,radius半径,diameter直径,arc弧。
例:
In the figure above,the radius of the circle with center o is 1and BC=1,what is the area of triangular region ABC?
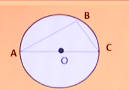
题干意思:上图圆中,半径是1,BC=1,那么三角形的面积是多少?
分析:r=1,AC=2.而且BC=1.根据圆内接三角形的性质可以知道,以圆的直径为一条边的圆内接三角形一定是直角三角形,那么AB=√3,所以面积是(√3)/2.
例:
In the circle above,angle PQO is 35 degrees,PQ is parallel to diameter OR,and OR has length 18,what is the length of minor arc PQ?
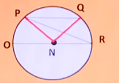
题干意思:在上图圆中,∠ PQO =35,PQ∥OR, OR=18,那么PQ最小弧长是多少?
分析:
弧长公式:规定n是圆心角度数,r是半径,l是圆心角弧长,α是弧度。
那么弧长L=n*π* r/180或者L=α* r
因为∠ PQO =35°,所以∠ QPR=35°连接PN和NQ,可知三角形PNR是等腰三角形,所以∠ RPN =35°所以∠ QPN =70°,三角形PNQ也是等腰三角形,所以∠ PQN =70°
所以∠ PNQ =180°-70*2=40°,因为 OR=18是直径,所以半径r=9,
所以弧长=40°*π*9/180°=2π。
例:
As shown in the figure above,a thin conveyor belt 15 feet long is drawn tightly around two circular wheels each 1 foot in diameter ,what is the distance ,in feet ,between the centers of the two wheels?
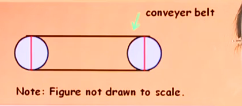
题干意思:
传送带的长度是15,圆形车轮的直径是1,那么两个圆形车轮圆心相距多少?
分析:
传送带长度=两个半圆的长度+两个直线的长度=15
也就是15=2πr+2L.所以L=(15-π)/2
例:
In the xy-plane,each point on circle K has nonnegative coordinates and the center of K is the point (4,7),what is the maximum possible area of K?
题干意思:在坐标轴中,一个圆上的所有点都在正数区域中(也就是第一象限中),圆心坐标是(4,7),那么圆的最大面积是多少?
分析:
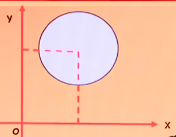
先画出这个圆,所以想要最大的面积,圆要和坐标轴相切,如果和X轴相切,这个圆就需要在第二象限中移动,所以不行,这个圆只能和Y轴相切,所以半径就是4,面积最大就是16π。
10、coordinate system坐标系,rectangular coordinate 直角坐标系
Origin 原点,abscissa 横坐标,ordinate 纵坐标,number line 数轴,quadrant象限,slope 斜率,intercept 截距(有正有负)。
例:
In the rectangular coordinate system above ,the area of triangular region PQR is ?
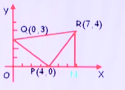
分析:我们可以补出一条垂直线构成一个直角梯形RNOQ,那么就可以用梯形的面积减去两个直角三角形的面积就等于所求的三角形PQR的面积了。最后三角形PQR面积是12.5。
例:
In the rectangular coordinate system above ,the area of PQR is what fraction (分数)of the area of △LMN?
分析:本题求的是三角形PQR 的面积是三角形LMN的面积的几分之几。
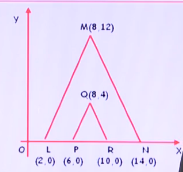
根据坐标可知他们的横坐标都是8,三角形顶点是一样的,根据面积=1/2底*高。所以答案是1/9.
以上就是关于GMAT数学突破51分必备题目分析之几何的内容介绍,复习GMAT需要耐力和耐心,无论是刚看的还是刷过几次的都要沉住气,利用好百利天下和其他各类资源,发现自己的问题,不要闷着做题,适当的时候总结一下事半功倍!大家继续加油,700+就在前方!
您还可能关注:



